標準偏差とは？求め方やデータ活用法を解説

標準偏差は、データの散らばり具合を示す物差しのようなものです。「平均値」はデータの真ん中を示しますが、標準偏差は、データが平均値からどれくらい離れているのかを示します。標準偏差は、一見難しそうに見える概念ですが、一度理解すれば、データ分析の幅が広がり、データドリブン経営などにも役立てられます。この記事では、標準偏差の基本的な考え方から、ビジネスシーンでの活用事例まで、わかりやすく解説します。

関連記事
・データドリブンとは？データドリブンマーケティング実現のために必要なことを解説
・データサイエンスとは！意味や概念をわかりやすく解説！

標準偏差とは

標準偏差とは、データのばらつきを示す重要な指標です。平均値からの差の標準値を表し、データの分布や特徴を簡潔に要約した数値です。

標準偏差を理解するには、まず「偏差」を正しく理解する必要があります。偏差とは、個々のデータと平均値との差の大きさです。平均値より「どのくらい大きいのか」もしくは「どのくらい小さいのか」といった、差の大きさを表します。

・偏差＝個々のデータ – 平均値（平均値からの差の大きさを表す）

例えば、平均点が48点のテストにおいて、生徒Aは65点、生徒Bは39点だった場合、それぞれ「+17点」と「-9点」が偏差です。

・生徒A（65点）の偏差：+17点
・生徒B（39点）の偏差：-9点

標準偏差は、偏差の標準値を意味します。これが理解できれば、全体のなかでのデータの位置関係を把握することが可能です。例えば、標準偏差が大きい場合は、データのばらつきが大きくなります。逆に小さい場合は、ばらつきが小さくなると判断できます。

また、正しく意味を理解することで、データを異なる見方で捉えられるようにもなります。先ほどの例では、平均点だけを見ると生徒Bの点数は「そこまで悪くない」と思うかもしれません。しかし、もし標準偏差が「3点」だとすると、生徒の多くは45点から51点の間の点数を獲得しているということになるため、生徒Bは「もっと勉強が必要」という評価ができます。

このように、「標準偏差」を理解していると、そのデータが特異的なのか、普遍的なのかをすぐに判断することが可能です。つまりデータが多ければ多いほど、正確な情報が得られるのです。ビジネスシーンにこの考え方を応用すれば、リスク管理や品質管理、データ分析などに活用することができます。

なお、一般的に用いられる形式として「標本標準偏差」と「母標準偏差」があります。両者の違いは、母標準偏差はすべてのデータが対象なのに対し、標本標準偏差は一部のデータから推定するという点です。

例えば、母集団が大きい場合や、反復して調査が可能な場合は、全数調査が難しいため、一部のデータから標準偏差を推定するのです。このようなケースでは、標本標準偏差を用います。

関連記事：母集団形成とは？新卒・中途採用を成功に導く入口を解説

標準偏差の計算方法

ここからは、具体例を挙げて標準偏差を計算する方法を解説します。

標準偏差の公式

分散については後ほど詳しく解説しますが、標準偏差は分散の平方根です。具体的には、以下の計算式で求められます。

標準偏差を求めるには、分散と平均値が必要です。それぞれの値は、下記の手順によって求められます。

1. 平均値を求める
2. 偏差を求める
3. 分散を求める
4. 分散の平方根を取る

具体例を挙げて、確認していきましょう。

平均値とは

平均値とは、対象となるデータの値をすべて合計し、データの個数で割った値です。例えば、生徒A・生徒B・生徒C・生徒D・生徒Eのテストの点数が下記の内容だった場合、平均点は次のようになります。

生徒	A	B	C	D	E
点数	70点	40点	60点	50点	30点

まずはデータの値をすべて足し、データの個数で割ることで、平均値を求められます。ここでは、生徒A・生徒B・生徒C・生徒D・生徒Eのテストの点数を足した250点を、データの個数である5で割った「50点」が平均点となります。平均値からは、データ全体の特徴を把握することが可能です。

分散とは

次は分散の計算です。分散とは、どのくらいデータが散らばっているのかを示す指標です。分散の値が小さいほど、データは平均値の中心に集まっており、値が大きいほど離れていることを表します。分散は以下の手順で求められます。

1. 平均値を求める
2. 偏差を求める
3. 偏差を二乗する
4. 3の結果を合計する
5. 4の結果をデータの個数で割る

例えば、生徒A・生徒B・生徒C・生徒D・生徒Eのテストの点数について考えてみましょう。前章で計算したとおり、平均値は「50点」です。これを基に偏差を求めると、下記のようになります。

生徒	A	B	C	D	E
偏差	+20点	-10点	+10点	0点	-20点

なお、偏差はすべて足すと0になります。そのため、分散を求める場合はマイナスの値をプラスにするために、二乗しなければなりません。各偏差の二乗を求めると、下記の通りです。

生徒	A	B	C	D	E
偏差の二乗	400	100	100	0	400

分散は偏差の二乗の平均でもあるため、上記を合計したものをデータの個数で割れば求められます。すなわち、以下の計算式で求めることが可能です。

ゆえに、生徒A・生徒B・生徒C・生徒D・生徒Eのテスト点数の分散は「200」となります。なお、分散は偏差を二乗して求めるため、元のデータと単位が異なります。そこで、元のデータと単位を合わせるため平方根を取ったものが標準偏差です。

すなわち、生徒A・生徒B・生徒C・生徒D・生徒Eのテスト点数の標準偏差は「約14点」となります。ここまでの流れを整理すると、標準偏差は下記の公式で求めることが可能です。

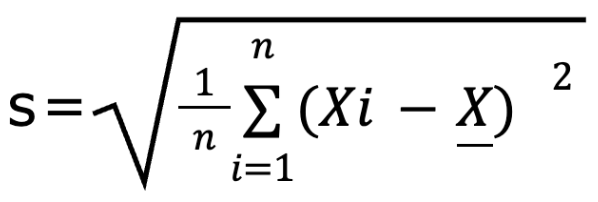
s：標本標準偏差
n：データの個数
Xi：各データの値
X：データの平均値

標準偏差の具体例

前章では、データのばらつきを示す標準偏差の計算方法を解説しました。もう一度おさらいしておくと、下記の手順に従って計算できます。

1. 平均値を求める
2. 偏差を求める
3. 分散を求める
4. 分散の平方根を取る

また、標準偏差によってデータを異なる見方で捉えられるようにもなるとお伝えしました。ここでは具体例を挙げて、標準偏差とデータの見方について解説します。

自宅（自転車/バス）から目的地までの到着例

まずは、自宅から目的地までの到着時刻に関する例を見ていきましょう。例えば、自転車とバスのどちらかを利用した場合、信号機や踏み切り、道の混雑状況など、日々の交通事情によって目的地への到着時刻の遅れが以下のようになったとします。自転車とバスのどちらを選択すればいいのでしょうか。

曜日	月	火	水	木	金
自転車	3分	2分	1分	2分	3分
バス	10分	1分	0分	0分	10分

平均値を求めると、自転車は平均「2.2分」の遅れ、バスは平均「4.2分」の遅れとなります。

	遅れの平均値
自転車	（3+2+1+2+3）÷5=2.2分
バス	（10+1+0+0+10）÷5=4.2分

平均値だけ見ると、2分の差であれば移動の楽なバスを選択する人が多いかもしれません。しかし、標準偏差を見てみると、印象は変わります。冒頭の手順に従い、標準偏差を計算してみましょう。

曜日	月	火	水	木	金
自転車の偏差	+0.8分	-0.2分	-1.2分	-0.2分	+0.8分
偏差の二乗	0.64	0.04	1.44	0.04	0.64

曜日	月	火	水	木	金
バスの偏差	+5.8分	-2.2分	-4.2分	-4.2分	+5.8分
偏差の二乗	33.64	4.84	17.64	17.64	33.64

	分散
自転車	（0.64+0.04+1.44+0.04+0.64）÷5=0.56
バス	（33.64+4.84+17.64+17.64+33.64）÷5=21.48

	標準偏差
自転車	√0.56≒0.748・・・・・・
バス	√21.48≒4.634・・・・・・

このケースだと、自転車は「平均2.2分+0.75分」で「3分弱」の遅れが予想されるのに対し、バスは「平均4.2分+4.63分」で「9分弱」の遅れが予想されます。標準偏差がわかれば、「9分弱」も遅れる可能性のあるバスを選ばない人は増えるかもしれません。

このように、標準偏差によって平均値だけでは見えてこなかったデータの捉え方ができるようになります。

野球投手の球速例

標準偏差は、野球投手のコントロールの良し悪しを判断するのにも役立ちます。例えば、A投手とB投手が的（まと）をめがけて5回ずつ投球した際の標準偏差を基に、コントロールの良さを考えてみましょう。ここでは話がわかりやすいように左右のずれは無視し、まとの中心を0としたときの上下のずれをもとに標準偏差を計算します。

	1球目	2球目	3球目	4球目	5球目
投手A	+40cm	-40cm	+15cm	+20cm	-30cm
投手B	+5cm	-5cm	-10cm	+10cm	+5cm

今回のケースでは的の中心が平均値でもあるため、上記は偏差でもあります。この偏差をもとに、冒頭の手順に従い標準偏差を計算してみましょう。

	1球目	2球目	3球目	4球目	5球目
投手Aの偏差	+40cm	-40cm	+15cm	+20cm	-30cm
偏差の二乗	1600	1600	225	400	900

	1球目	2球目	3球目	4球目	5球目
投手Bの偏差	+5cm	-5cm	-10cm	+10cm	+5cm
偏差の二乗	25	25	100	100	25

	分散
投手A	（1600+1600+225+400+900）÷5=945
投手B	（25+25+100+100+25）÷5=55

	標準偏差
投手A	√945≒30.74・・・・・・
投手B	√55≒7.41・・・・・・

結果として、投手Aの標準偏差は「±30.7cm」、投手Bの標準偏差は「±7.4cm」となりました。前述の通り大きいほどデータのばらつきは大きく、小さいほどデータのばらつきは小さいことから、標準偏差の小さい投手Bのほうがコントロールに優れた投手だということになります。

標準偏差で注意すること

続いて、標準偏差を解釈する上で注意すべきポイントを解説します。

標準偏差が0に近いという意味

標準偏差が0に近い場合は、データ全体の値が平均値に近いことを意味します。前述の通り、大きいと平均値との差が大きく、小さいと平均との差が小さいと判断することが可能です。すなわち、平均との差が小さくデータのばらつきが非常に小さいということになります。

データの一貫性が高い

標準偏差が0に近いとデータのばらつきが非常に小さいため、データの一貫性が高いと判断できます。例えば、製造業において一貫性のある製造プロセスが確立されており、ほぼ同じ寸法の製品が製造されている場合、寸法の標準偏差は限りなく0に近くなります。品質管理の観点からみると製造プロセスが安定しており、非常に理想的な状態です。

ばらつきが欠如している

別の見方をすると、標準偏差が0に近しい場合は、ばらつきが欠如している状態です。現実世界において、標準偏差が正確に0である完全な一貫性は実現できません。しかし、極めて0に近い場合は、すべてのデータがほぼ同じであると判断することが可能です。例えば、アンケート調査で全員の意見が非常に近しいケースや、一貫性の非常に高い製造プロセスが確立されているケースなどが考えられます。

標準偏差0が好ましいとは限らない

ただし、標準偏差の意味を解釈する場合、必ずしも0が好ましいとは限らない点には注意が必要です。

例えば、アンケート調査やブレインストーミングなど、多様性や創造性が求められる場面では、標準偏差が0に近いと調査や議論が十分ではなく、多様性や創造性が発揮できていない可能性があります。標準偏差の意味を解釈する場合は、対象となるデータの背景や文脈を考慮することが重要です。

関連記事：KJ法とは？発想法としてのやり方やメリットを解説

データの特徴を知る

正規分布に従うデータは、平均値から±標準偏差1個分の範囲に約68％が、±標準偏差2個分の範囲に約95％が含まれるという特徴があります。正規分布とは、「平均値＝最頻値＝中央値」が成り立ち、平均値を軸に左右対称になっている確率分布です。

標準偏差の2倍は重要な意味を持つ

正規分布に従うデータは上記のような特徴があるため、標準偏差の2倍は非常に重要な意味を持ちます。標準偏差の2倍という考え方は、データの広がりがどの程度かを把握するための指標です。

すべてのデータが正規分布の形を取るわけではない

すべてのデータが正規分布の形を取るわけではないため、2倍の意味を解釈する際には注意が必要です。例えば、データが歪んでいる場合や特異なデータが含まれる場合は、標準偏差を2倍してもデータの分布を正確に把握することはできません。

データの分散を把握する上で標準偏差の2倍という考え方は概ね有効ですが、データの形状や背景・文脈にも依存するため、意味の解釈には慎重さが必要です。

ビジネスシーンでよく使う標準偏差

ここまで解説してきた通り、標準偏差はデータのばらつきを示す指標です。統計学の基礎である基本統計量の一つでもあり、私たちの日常でもさまざまな場面で用いられています。例えば、集団のなかでの位置関係を表す偏差値は、標準偏差を応用した代表例です。ここでは、ビジネスシーンでの標準偏差の活用例を詳しくご紹介します。

データ分析

データドリブン経営の推進が叫ばれる昨今、あらゆるデータを基に経営戦略を立案・実行する企業が増えています。ビジネスシーンにおけるデータは、平均値や属性だけでなく、標準偏差を把握することも重要です。

例えば、店舗Aと店舗Bがあり、各店舗の平均売上は同じだったとします。しかし、売上について標準偏差を見ると、店舗Aは10、店舗Bは100だった場合、店舗Aは売上のばらつきが小さく、安定して売上を出せていることがわかります。

また、商品Cと商品Dの満足度について、100点満点で点数をつけるアンケート調査を実施した場合、平均点は同じ60点だったとします。しかし、満足度の標準偏差を見たときに、商品Cは10だったのに対し、商品Dは30だったことがわかりました。商品Cは多くのユーザーが50点から70点と評価したのに対し、商品Cは90点の高評価もあった一方、一部のユーザーからは30点の低評価を受けていたことがわかったのです。

このように、たとえ平均値が同じであっても、標準偏差を見ると印象ががらりと変わるケースも少なくありません。平均値だけでなく、標準偏差を知ることでデータの特徴を把握できるため、より効果的な経営戦略を立案・実行することができるでしょう。

関連記事：アンケートの正しい作り方｜効果的に回収するコツや基本形式、例文

リスク管理

ビジネスシーンでは、リスク管理においても標準偏差を知ることは非常に重要です。ビジネスにおいて何らかの経営判断を下す場合、リスクを伴うケースも少なくありません。プロジェクトや取引にもよりますが、結果にばらつきがあると、一般的にそのビジネスはハイリスクとなります。

株式投資においては、株価変動の標準偏差を求めて意思決定に役立てることも可能です。例えば、株価変動について標準偏差が10の銘柄と100の銘柄があった場合、標準偏差が10の銘柄は株価の変動が小さく、安定した銘柄といえます。一方、標準偏差が100の銘柄は株価の変動が大きく、ハイリスクハイリターンの銘柄です。少しでもリスクを抑えて投資をしたい場合は標準偏差10の銘柄を、リスクがあっても大きなリターンを狙いたい場合は標準偏差100の銘柄を選択する、という判断ができます。

また、商品の売上予測を立てる場合も、標準偏差が有効です。例えば、一日100個売れる商品があり、販売個数について標準偏差が30だったとします。売り上げが良い日は130個、売り上げが悪い日は70個売れる予測が立てられるため、仕入れの判断に役立てることが可能です。標準偏差に基づいて商品を発注すれば、過剰在庫や在庫切れのリスクを軽減できます。ただし実際の発注量は、欠品を許容できるかどうかで判断するのが一般的です。具体的には、日持ちがしない生鮮食品などは在庫リスクを考えて、ある程度長期間在庫を抱えられる日用品などは欠品リスクを考えて、発注量を判断することになります。

標準偏差を知ることで、予想される利益を数値化して予測できるため、経営判断に伴うリスクをコントロールすることが可能です。

関連記事：リスクヘッジとは？ビジネスにおける意味とやり方

品質管理

品質管理においても、標準偏差の考え方は非常に重要です。製造業などにおいて、製造プロセスを標準化したとしても、商品の品質にばらつきが生じることは避けられません。多少のばらつきは誤差として許容されるケースもありますが、誤差が大きいとクレームにつながる可能性があるので、慎重さが必要です。

寸法や質量の個体差をどの程度許容できるのか、どの程度の誤差があると規格外になるのかといった予測を立てる際に、標準偏差が用いられます。例えば、一辺が5cmの部品を製造する場合、あるものは4cm95mm、またあるものは5cm5mm、といったように、個体差が大きいと品質が良いとは言えません。粗悪品は企業の信用を毀損する原因ともなるため、標準偏差があまりに大きいようであれば、製造プロセスや検査フローを見直す必要があるでしょう。

前述の通り、標準偏差は正規分布に従う場合、平均値から±標準偏差1個分の範囲にデータの約68％が、±標準偏差2個分の範囲にデータの約95％が含まれるという特徴があります。正規分布とは、平均値を軸に左右対称になっている確率分布で、統計学ではもっとも代表的な分布の一つです。標準偏差の特徴を活用し、寸法や質量が平均値から±標準偏差2個以上離れている個体を規格外とする方法があります。

このようなケースにおいては、標準偏差によってばらつきを数値化することで、品質を担保することが可能です。

関連記事：なぜなぜ分析とは？意味とやり方、コツ、手順を解説

マーケティングで活用する標準偏差とは

マーケティングの分野においても、標準偏差は非常に重要な指標の一つです。例えば、顧客の購買行動を標準偏差によって分析することで、購買の傾向や嗜好のばらつきを把握できます。

顧客の傾向や嗜好を把握できれば、よりターゲットに最適なマーケティング施策を実行することが可能です。顧客セグメンテーションに基づくターゲットマーケティングや、さまざまな顧客データを基に戦略を立案・実行するデータドリブンマーケティングに、標準偏差は欠かせません。

また、異なる複数のマーケティング施策を立案・実行し、効果を測定するような場面でも、標準偏差によって効果のばらつきを分析することが重要です。例えば、商品の購買を促すインターネット広告を出稿する場合、購買意欲の変化について標準偏差を調べて過去の実績と比較することで、広告の効果を相対的に評価できます。

前章でも述べた通り、売上予測や顧客満足度といったデータ分析、経営判断に伴うリスク管理、企業の信用を維持・向上するための品質管理などにおいても、標準偏差は必須の指標です。

統計学に慣れていないマーケターにとって、標準偏差は少し分かりにくい考え方かもしれませんが、標準偏差を積極的に活用することで、マーケティング施策の効果を最大化することが可能です。

関連記事
・マーケティングとは？基礎や重要ポイントを初心者にも分かりやすく解説
・マーケティング戦略とは？立案手順やフレームワーク、成功事例を解説
・ターゲティングとは？戦略的なターゲット設定の方法と成功例
・顧客セグメンテーションとは？概要や分類例、実践方法まで解説！
・CS（カスタマーサティスファクション）とは？顧客満足度向上のための施策や具体例

まとめ

標準偏差とは、データのばらつきを示す指標です。統計学の基礎である基本統計量の一つで、標準的な平均値との差の大きさとも言い換えられ、平均値と分散によって求められます。標準偏差を知ることでデータの分布や特徴を把握することが可能です。

ビジネスシーンやマーケティングにおいても、標準偏差の考え方は欠かせません。特に、リスク管理や品質管理、データ分析などの分野においては、標準偏差による分析は非常に効果的です。標準偏差の考え方を正しく理解し、ビジネスやマーケティングに積極的に活用していきましょう。